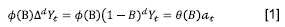
DOI: 10.18041/2619-4244/dl.34.11649

Análisis de contagios SARS COV-2 por medio de herramientas de series de tiempo

Time series analysis for SARS COV-2 infections

David Santiago Alzate Vélez
Ingeniero financiero
Instituto Tecnológico Metropolitano de Medellín
Correo: davidalzate220456@correo.itm.edu.co

Luisa Fernanda Rojas Metaute
Ingeniero financiero
Instituto Tecnológico Metropolitano de Medellín
Correo: luisarojas213893@correo.itm.edu.co

William Fernando Correa Serna
Ingeniero financiero
Instituto Tecnológico Metropolitano de Medellín
Correo: williamcorrea199727@correo.itm.edu.co

David Esteban Rodríguez Guevara
Magíster en Administración financiera
Instituto Tecnológico Metropolitano de Medellín
Correo: davidrodriguez@itm.edu.co

Como citar: Alzate Vélez, D. S., Rojas Metaute, L. F., Correa Serna, W. F., & Rodríguez Guevara, D. E. (2024). Análisis de contagios SARS COV-2 por medio de herramientas de series de tiempo. Dictamen Libre, (34: Enero-Junio). pp.15-24. https://doi.org/10.18041/2619-4244/dl.34: Enero-Junio. 11649

RECIBIDO 30 de noviembre de 2023 ACEPTADO 11 de abril de 2024

Resumen

El presente artículo analiza y desarrolla herramientas de series de tiempo con las cuales se pueda estimar la curva de contagios de SARS-COV2 en países de Latinoamérica. Para este estudio se toma una muestra de contagios diarios de casos positivos en diez países. Para su desarrollo se utilizaron los modelos econométricos, ARIMA, ARFIMA y NNAR, a los cuales se les realizaron diversas estimaciones establecer el que más se ajustara a la serie a partir de la medición de los criterios de bondad de ajuste. El resultado de este estudio demuestra que por medio de los modelos de NNAR se puede pronosticar de forma más acertada y precisa la curva de contagios de Covid-19 en Latinoamérica.

Palabras clave: ARIMA, ARFIMA, redes neuronales, SARS-COV2, Covid-19, series de tiempo.

Abstract

This article analyzes and develops time series tools with which the SARS-COV2 infection curve can be estimated in Latin American countries. For this study, a sample of daily infections of positive cases in ten countries is taken. For its development, the econometric models ARIMA, ARFIMA and NNAR were used, to which various estimates were made to establish the one that best fit the series based on the measurement of the goodness-of-fit criteria. The result of this study demonstrates that through NNAR models the Covid-19 infection curve in Latin America can be predicted more accurately and precisely.

Keywords: ARIMA, ARFIMA, Neural Networks, SARS-COV2, Covid-19, time series.

INTRODUCCIÓN

El 16 de marzo de 2020 la OMS (2020a) decretó que "…la pandemia de la Covid-19 es una emergencia sanitaria y social mundial". Hasta el 10 de septiembre de 2021, se registraron en América Latina y el Caribe un total de 43 millones de casos, Siendo Brasil el país más afectado en la región, con cerca de 20.9 millones de casos confirmados. Seguido de Argentina, con aproximadamente 5.2 millones de infectados. México, por su parte, registra un total de 3.479.999 casos (Statista Research Department, 2021). El 1.° de septiembre de 2021, la OPS (2021b) advirtió que el 75% de la población de América Latina y el Caribe aún no está totalmente vacunada contra la Covid-19 e informó que la OPS está acelerando sus esfuerzos para ampliar el acceso a las vacunas en toda la región (OPS, 2021a; Orús, 2021).

La aplicación de modelos estadísticos para predecir el número de infectados por esta enfermedad en una nación se ha vuelto de gran interés. Kartikasari et al. (2020) estimaron los casos futuros positivos y muertes por Covid-19 en Indonesia, mostrando la eficiencia de estimación de dichos modelos. Por su parte, Pinzón (2021) dio a conocer el modelo ARIMA para pronosticar el tiempo de inmunidad de rebaño, con el cual sugiere que para el 19 de enero de 2022 se logrará obtener la inmunidad de rebaño. Hamadneh et al. (2021) presentan un artículo en el que utilizan redes neuronales artificiales (ANN) para predecir el número de casos de Covid-19 en Brasil y México durante ciertos días. El estudio muestra el número esperado de infecciones, recuperaciones y muertes que Brasil y México alcanzarán diariamente a principios de 2021.

Desde el momento en que se detectó por primera vez el Covid-19 hasta principios de mayo de 2020, el virus se había propagado a 216 países infectando a más de 4 millones de personas, con más de 300.000 muertes registradas (Alabdulrazzaq et al., 2021; Ala'raj et al., 2021). Esto genera la necesidad de hacer un estudio y análisis de los comportamientos del virus, que puede llegar a ser medible. Una predicción acertada del número de contagios ayudaría a los responsables políticos de una región concreta a evaluar su infraestructura sanitaria actual y a establecer las medidas que deben adoptarse para detener y controlar la difusión del Covid-19 (Alabdulrazzaq et al., 2021).

Revisando estudios previos, se encuentra a Dehesh et al. (2020), quienes predicen con modelos ARIMA a partir de datos de casos confirmados, con el fin de tener una mayor preparación en los sistemas de salud. El estudio de Ilie et al. (2020) muestra que los modelos de series de tiempo ARIMA se aplicaron con éxito para estimar la prevalencia general de Covid-19 en nueve países. Kartikasari et al. (2020) demuestran que el ARFIMA (1,0.431,0) es el mejor modelo para predecir los datos sobre la adición de nuevos casos de pacientes que mueren por Covid-19. Adesina et al. (2020) utilizan el modelo de Media Móvil Integrada (ARFIMA) para predecir la tendencia de los casos confirmados en Argelia, obteniendo resultados eficientes de predicción.

Este artículo se desarrolla con los modelos ARIMA, ARFIMA y NNAR, realizando varias estimaciones para determinar cuál se ajusta mejor a la serie. Esto se establece por medición de los criterios de bondad de ajuste. Del sitio web https://ourworldindata.org/ coronavirus se toman los casos positivos confirmados por Covid-19 en Latinoamérica entre el 23 de febrero de 2020 y el 15 de septiembre de 2021. El principal objetivo de este estudio es determinar el comportamiento del Covid-19 en Latinoamérica.

Con base en los estudios revisados y en los modelos definidos; dos basados en modelos paramétricos univariados (ARIMA y ARFIMA) y otro en un sistema de predicción genética, como una red neuronal autorregresiva (ANN) (Niazkar & Niazkar, 2020), pretende responder el siguiente interrogante: ¿Qué modelo puede predecir con mayor precisión la curva de contagios de Covid-19 (SARS-COV2) en Latinoamérica?

MATERIALES Y MÉTODOS

A continuación, se muestran los modelos que se implementarán para medir la evolución diaria del Covid (Velásquez & Franco, 2012).

Modelo ARIMA

De la Fuente Fernández (2016) indica que este modelo permite describir un valor como una función lineal de datos anteriores y errores debidos al azar, puede incluir un componente cíclico o estacional y debe contener todos los elementos necesarios para describir el fenómeno. Los pasos para realizar un modelo ARIMA son: 1) Transformar la serie observada en una serie estacionaria o determinar un modelo ARMA para la serie estacionaria. 2). Estimar los parámetros AR y MA y obtener los errores del modelo. 3) Realizar el diagnóstico en el que se comprueba que los residuos no tienen estructura de dependencia y siguen un proceso de ruido blanco. 4) Una vez obtenido el modelo adecuado se realizan las predicciones. Se define ARIMA como en la ecuación [1], donde Δ^d Y_t= (1-B)^d Y_t es un proceso estacionario, d es un número entero positivo, B es el operador de retardo, {α} es un proceso de ruido blanco con distribución N(0.σ²) y los términos Φ(B)=1-Φ₁ B-Φ₂ B² corresponde a la parte autorregresiva y media móvil, respectivamente.

Modelo ARFIMA

Brockwell & Davis (2002) consideran que un procedimiento estocástico Z_t es un proceso ARFIMA (p, d, q) si es una solución a la ecuación [2], donde Φ(B) = 1 - Φ₁ B - … - Φ_P B^P y θ(B)=1-θ₁ B…-θ_q B^q son, respectivamente, los polinomios autorregresivos y de medias móviles de orden p y q de un proceso ARMA, cuyos ceros están fuera del círculo unidad y no tienen raíces comunes; d y θ₀ son números reales; d es llamado el parámetro de diferenciación fraccional; α_t son variables aleatorias no observables independientes e idénticamente distribuidas con media cero y varianza finita σ². Castaño (2016) demostró que si d>-0,5 y todas las íaíces de θ(B)=0 caen fuera del círculo unidad, Z_ts un proceso invertible; si d<-0,5 y todas las raíces de Φ(B)=0 caen fuera del círculo unidad, Z_t es un proceso estacionario. Por tanto, el proceso ARFIMA (p, d, q) es estacionario e invertible si todas las raíces de θ(B)=0 y Φ(B)=0 caen fuera del círculo unidad y -0,5<d<0,5.

Redes Neuronales

Las redes neuronales son modelos computacionales que imitan las redes de neuronas del cerebro con el fin de emular el comportamiento inteligente (Velásquez & Franco, 2012; Velásquez, H., 2011). Según Flórez (2008), para desarrollar un modelo de red neuronal autorregresivo los rezagos definidos se pueden utilizar como variables de entrada, de la misma manera como se utilizan en los modelos de predicción de autorregresión lineal (Martin & Pineros, 2020). La aplicación de estos modelos se ha definido en cinco etapas: 1) búsqueda de las variables, 2) preparación del conjunto de datos, 3) creación de la red, 4) entrenamiento y 5) validación (Floréz López & Fernández Fernández, 2008). Como se muestra en [3], donde β^* es el peso de la conexión de la neurona adaptativa a la neurona de salida, βh es el peso asociado a la conexión entre cada neurona h de la capa oculta y la neurona de salida, ωh respresenta el peso de las conexiones que van de la neurona adaptativa hasta cada neurona h de la oculta, αi,h pesos entre cada entrada i y la neurona h en la capa oculta, H representa el número de neuronas en la capa oculta, p es el número de rezagos considerados y g es la función de activación de las neuronas de procesamiento en la capa oculta.

Criterios de bondad de ajuste

Castaño (2016) muestra que para ver la adecuación que existe entre la serie real y la estimada se puede utilizar el coeficiente de determinación o el coeficiente de determinación corregido, así como los criterios de Schwartz y de Hannan Quinn. Bielsa (2016) propone el criterio de información de Akaike (AIC, criterio de información corregido (AICc)), ME (mean error), MAE (mean absolute error), MPE (mean percentage error), MAPE (mean absolute porcentage error), MASE (mean absolute porcentage error) y RMSE (root mean squared error).

RESULTADOS

La información que se va a analizar e interpretar con el modelo son los datos de los contagios nuevos en Latinoamérica, tomados del sitio web oficial https://ourworldindata.org/coronavirus. La serie inicia el 23 de febrero de 2020 y va hasta 15 de septiembre de 2021, con una frecuencia diaria. Después de construir la base de trabajo se realizan cálculos de algunas estadísticas descriptivas (t para identificar las variaciones y el comportamiento de cada una de las variables de este estudio, que en este caso son los países de Latinoamérica.

De acuerdo con la tabla anterior (tabla 1), los datos máximos de contagios nuevos en un día se encuentran en Brasil, Argentina, Colombia y México, lo cual es coherente con el orden de países con más casos reportados. Los países con promedio de casos más bajo son Uruguay y Paraguay, que oscilan entre 700 y 800 casos diarios. De estos últimos tres países Paraguay exhibe que su desviación de casos con respecto a su promedio es de 837.01. En cuanto a la estadística de la información presentada, se observa que Uruguay presenta mayor variación, con un coeficiente igual a 1.63, mostrando datos heterogéneos (Statista Research Department. 2021).

A continuación, se evidencia el desarrollo y análisis de los modelos de series de tiempo utilizados para el desarrollo de este trabajo.

Modelo ARIMA

Al realizar la comparación de diferentes modelos ARIMA para cada país, se observan los modelos seleccionados, que se determinaron por análisis de bondad de ajuste y la significancia de sus coeficientes (tabla 2). De los modelos comparados para Brasil, con base en los criterios RMSE y ME, el modelo ARIMA (3,1,1) presenta los menores valores en este criterio, en comparación con los otros dos modelos estimados.

Respecto a Colombia, se estimaron los modelos ARIMA (2,1,1), (2,1,4) y (1,1,3), de los cuales se seleccionó el modelo ARIMA (2,1,1), a pesar de que el modelo (2,1,4) presentó valores menores en los criterios RMSE y ME, sus coeficientes M1, AR1 y AR2 presentan valores que dejan de ser significativos a la hora de hacer la selección del mejor modelo que ajuste los datos.

Modelo ARFIMA

En la siguiente tabla (tabla 3) se observan las estimaciones de los parámetros de los mejores modelos ARFIMA para cada país. Todos los modelos arrojan un parámetro de diferenciación fraccional entre [-0.5 y 0,5], indicando que las series en estudio tienen una dinámica de memoria de largo plazo. En Brasil, por su parte, con la estimación de los modelos ARFIMA (2,0.40,0), (1,0.37,1) y (3,0.45,0) para la selección del modelo con mejor ajuste, se analiza el p-valor de los diversos parámetros en los modelos, estableciendo que el modelo (3,0.45,0) al presentar un p-valor en el parámetro AR1 mayor a 0,05 pierde significancia estadísticamente, a pesar de presentar un valor menor de bondad de ajuste en comparación con los otros dos modelos. El modelo seleccionado (2,0.40,0) presenta un RMSE de 15719.23 y un ME 38.87, lo cual significa que es que menos se desvía de los datos originales.

Redes Neuronales (NNAR)

Durante la ejecución del modelo de Red Neuronal para cada serie se estableció una cantidad de 30 nodos para la capa oculta, teniendo en cuenta que estas series presentan una temporalidad secuencial diaria. En cada serie se establecieron diez repeticiones, mostrando un mejor procesamiento al momento de arrojar resultados. Para Brasil se realizaron tres simulaciones con diferentes repeticiones (1,5 y 10), evidenciando que con diez repeticiones esta muestra una red más entrenada y unos datos más precisos en comparación con las otras dos simulaciones.

En lo referente a la varianza de los modelos, Brasil, Perú y México arrojan un σ^∧2 de proporciones altas, lo que significa que estos países presentan una mayor volatilidad. El único indicador que asume la determinación del ajuste para estos tres países es el MASE, con un valor <1.

Comparación y elección de modelos, según su medición

Inicialmente se tomó una muestra de los contagios positivos en Latinoamérica hasta el 15 de septiembre del 2021,a partir de los cuales se desarrolló un entrenamiento de los datos, estimando los modelos que mejor se ajustaran a la serie. Posteriormente, se revisó la eficiencia de los modelos mediante una prueba, con los datos más recientes hasta el 31 de octubre del 2021, analizando sus residuales y la medición de criterios de bondad de ajuste.

Después de ejecutar los modelos ARIMA, ARFIMA y NNAR se compararon los resultados obtenidos de las diez series de tiempo, logrando establecer el modelo que mejor se ajustaba los datos para cada país. En la siguiente tabla (tabla 5) se evidencia que las diez series de tiempo obtuvieron un mejor ajuste con NNAR, con base en los resultados obtenidos de sus residuales. Brasil presenta el valor más alto en el índice RMSE y MAE en los modelos ARIMA y ARFIMA, en comparación con el resto de países. El modelo de NNAR es el de mejor ajuste para esta serie, con índices de RMSE de 1324.07 y MAE de 1324.07, aunque estos dos criterios presentan valores iguales en el caso de Brasil.

Por su parte, México presenta un comportamiento similar entre ARIMA y ARFIMA, pero para el caso de la medición de los criterios de bondad de ajuste del modelo ARFIMA estos presentan unos índices mayores a los del modelo ARIMA. Al igual que el comportamiento de las demás series, se evidencia que el modelo de NNAR estudia de mejor manera los datos de este país. Verificando los modelos estudiados, se puede concluir que se puede hacer un pronóstico más acertado con el modelo de NNAR.

Al analizar el criterio MASE, se evidencia que el modelo de NNAR presenta índices en las series que se aproximan a 0, en comparación con ARIMA y ARFIMA, que tienen tendencia a 1, demostrando que el modelo de NNAR realiza un ajuste más preciso con la prueba de eficiencia de los modelos. Esto da la certeza de que el modelo de NNAR puede realizar un pronóstico más acertado a la realidad de los casos futuros por Covid-19 en Latinoamérica.

CONCLUSIONES Y RECOMENDACIÓN

En la implementación de los modelos ARIMA se evidencia que en las estimaciones del modelo que mejor se ajusta a los datos de cada país en estudio, Brasil presenta los criterios de bondad de ajuste más altos. Con los modelos estimados para cada serie de tiempo se puede afirmar que el modelo ARIMA no es apropiado para lograr una predicción real de los casos futuros de Covid-19 en Latinoamérica, puesto que presenta unos índices muy elevados, dando certeza que no se logra un ajuste preciso.

Con los datos obtenidos a través de los modelos de NNAR se puede afirmar que este modelo tiene una precisión más acertada de los datos en estudio, puesto que los criterios de bondad de ajuste muestran valores mucho más bajos, dando más confiabilidad a las predicciones realizadas. Los resultados y análisis determinan que por medio de los modelos de NNAR se puede pronosticar de forma más acertada y precisa la curva de contagios de Covid-19 en Latinoamérica.

AGRADECIMIENTOS

Los autores agradecen al Instituto Tecnológico Metropolitano de Medellín y a la Facultad de Ciencias Económicas y Administrativas por la oportunidad del proceso académico y de investigación.

CONFLICTO DE INTERESES

Los autores de este artículo manifiestan la independencia en su proceso de investigación y redacción, y no tener ningún conflicto de intereses.

REFERENCIAS

Adesina, O. S., Onanaye, S. A., Okewole, D., & Egere, A. C. (2020). Forecasting of New Cases of COVID-19 in Nigeria Using Autoregressive Fractionally Integrated Moving Average Models. Asian Research Journal of Mathematics, 135-146. https://doi.org/10.9734/arjom/2020/v16i930226.

Alaraj, M., Majdalawieh, M., & Nizamuddin, N. (2021). Modeling and forecasting of COVID-19 using a hybrid dynamic model based on SEIRD with ARIMA corrections. Infectious Disease Modelling, 6, 98-111. https://doi.org/10.1016/j.idm.2020.11.007.

Alabdulrazzaq, H., Alenezi, M. N., Rawajfih, Y., Alghannam, B. A., Al-Hassan, A. A., & Al-Anzi, F. S. (2021). On the accuracy of ARIMA based prediction of COVID-19 spread. Results in Physics, 27. https://doi.org/10.1016/j.rinp.2021.104509

Bielsa, F. J. T. (2016). bibliotecaitm. Introducción a la econometría. https://elibro-net.itm.elogim.com:2443/es/lc/bibliotecaitm/titulos/49156.

Brockwell, P. J. & Davis, R. A. (2002). Introduction to Time Series and Forecasting - Second Edition. In Springer-Verlag. http://books.google.com/books?id=9tv0taI8l6YC

Castaño, E. (2016). De modelos ARFIMA a ON IDENTIFICATION IN ARFIMA MODELS. 12-37.de la Fuente Fernández, S. (2016). Series Temporales: Modelo Arima. Universidad Autónoma de Madrid, 1-14. http://www.estadistica.net/ECONOMETRIA/SERIES-TEMPORALES/modelo-arima.pdf.

Dehesh, T., Mardani-Fard, H. A., & Dehesh, P. (2020). Forecasting of COVID-19 Confirmed Cases in Different Countries with ARIMA Models. MedRxiv, 1-12. https://doi.org/10.1101/2020.03.13.20035345

Floréz López, R., & Fernández Fernández, J. M. (2008). Las Redes Neuronales Artificiales.

Florez, R. (2008). Las Redes Neuronales Artificiales.

Hamadneh, N. N., Tahir, M., & Khan, W. A. (2021). Using artificial neural network with prey predator algorithm for prediction of the COVID-19: The case of Brazil and Mexico. In Mathematics (Vol. 9, Issue 2, pp. 1-14). https://doi.org/10.3390/math9020180.

Ilie, O. D., Cojocariu, R. O., Ciobica, A., Timofte, S. I., Mavroudis, I., & Doroftei, B. (2020). Forecasting the spreading of COVID-19 across nine countries from Europe, Asia, and the American continents using the arima models. Microorganisms, 8(8), 1-19. https://doi.org/10.3390/microorganisms8081158.

Kartikasari, P., Yasin, H., & Asih I Maruddani, D. (2020). ARFIMA Model for Short Term Forecasting of New Death Cases COVID-19. E3S Web of Conferences, 202. https://doi.org/10.1051/e3sconf/202020213007.

Martín, R., & Piñeros, L. (2020). Propuesta de un modelo con redes neuronales y metodología Box & Jenkins para el pronóstico del precio de bolsa de la energía en Colombia. 57. https://repository.libertadores.edu.co/handle/11371/2654#.X3xvnsLRlJA.mendeley

Niazkar, H. R., & Niazkar, M. (2020). Application of artificial neural networks to predict the COVID-19 outbreak. Global Health Research and Policy, 5(1). https://doi.org/10.1186/s41256-020-00175-y.

OMS (2020). COVID-19: cronología de la actuación de la OMS. In Organización Mundial de la Salud.

OPS (2021a). Controlar la COVID-19 en las Américas podría llevar años si continúa el ritmo lento de vacunación actual, advierte la directora de la OPS - OPS/OMS | Organización Panamericana de la Salud. Controlar.

OPS. (2021b). OPS: sólo una de cada cuatro personas está completamente vacunada contra la COVID-19 en América Latina y el Caribe - OPS/OMS | Organización Panamericana de la Salud. OPS:.

Orús, A. (2021). Casos confirmados de coronavirus en el mundo por continente 2021 | Statista. Número de Casos Confirmados de Coronavirus a Nivel Mundial a Fecha de 12 de septiembre de 2021, por continente.

Pinzón, J. E. D. (2021). Perspectiva del tiempo para alcanzar la inmunidad de rebaño para COVID-19 a nivel mundial. Revista Repertorio de Medicina y Cirugía, 30, 73-78. https://doi.org/10.31260/REPERTMEDCIR.01217372.1245.

Statista Research Department (2021). Coronavirus en Latinoamérica: países con más casos | Statista. Número de Casos Confirmados de Coronavirus (COVID-19) En América Latina y El Caribe al 10 de septiembre de 2021, por país.

Velásquez-H., J. D. (2011). Acotación del error de modelos de redes neuronales aplicados al pronóstico de series de tiempo. Revista UIS Ingenierías, 10(1), 63-69.

Velásquez, J. D., & Franco, C. J. (2012). Pronóstico de series de tiempo con tendencia y ciclo estacional usando el modelo airline y redes neuronales artificiales. Ingeniería y Ciencia, 8(15), 171-189. https://doi.org/10.17230/ingciencia.8.15.9.