Redes neuronales artificiales aplicadas en sistemas de predicción para la seguridad vial
Artificial neural networks applied in prediction systems for road safety
Artículos
Recibido: 15/08/2020
Aprobado: 24/10/2020
Autores
Carpio Peláez Karina Patricia
Oñate- Valdivieso Fernando
Resumen
En esta investigación se aplican redes neuronales artificiales para el análisis de variables que podrían tener influencia en la ocurrencia de accidentes de tránsito en carreteras de montaña. El modelo se desarrolló utilizando Redes Neuronales Artificiales (RNA) y se evaluó su eficiencia para la predicción de accidentes de tránsito considerando variables como radios de curvatura y pendientes de la vía. El desempeño de las Redes Neuronales Artificiales se evaluó aplicando la eficiencia de Nash- Sutcliffe y en el error cuadrático medio. Los resultados de la investigación mostraron un bajo desempeño de las Redes Neuronales Artificiales en el pronóstico de accidentes en función de las variables seleccionadas, lo que sugiere que los accidentes aparentemente no se deben a la geometría de la vía, o topografía, geografía del terreno, sino a otros elementos tales como el exceso de velocidad o la impericia del conductor. Sin embargo, la investigación muestra varias alternativas de modelamientos de la Red para intentar tener una mejor predicción
Abstract
Artificial neural networks (ANN) are applied in this research for the analysis of variables that could influence the occurrence of traffic accidents on mountain roads. The model was developed through Artificial Neural Networks (RNA), and its efficiency was evaluated for the prediction of traffic accidents considering variables as radio of curvature and track slopes. RNA performance was evaluated by applying the Nash-Sutcliffe efficiency and the mean quadratic mistake. The results of the research showed a low performance of the RNA in the prediction of accidents according to the selected variables, which suggests that accidents do not appear to be due to track geometry, but to other elements such as speeding or driver’s sleight of hand. However, the research provides several alternatives for modeling the Network to achieve a more accurate prediction
1. Introducción
Los accidentes de tránsito, son un gran problema de salud pública, cada año mueren cerca de 1,2 millones de personas en las carreteras del mundo entero, y entre 20 y 50 millones padecen traumatismos no mortales [1]. La mayoría de estas muertes se dan en países de bajos y medianos ingresos por el rápido crecimiento económico que tiene el estado, acompañado de un aumento de motorización y traumatismos causados por el tránsito [1]. Los accidentes de tránsito son una de las principales causas de muerte en todos los grupos etarios, y la primera entre personas de entre 15 y 29 años. En las carreteras interprovinciales del Ecuador han aumentado considerablemente los accidentes de tránsito, así, en el año 2014, se registraron en el país 38.658 accidentes de tránsito[17]. El promedio por mes fue de 3.2, siendo junio el mes con mayor número de accidentes con el 9.8% respecto del total. La provincia del Pichincha registró el mayor número de accidentes con el 39%, siguiéndole la provincia del Guayas con el 25% y en tercer lugar la provincia de Tungurahua con el 5% [2]. En el Ecuador a pesar de tener el 1% menos de población mundial, tiene el 2% en víctimas de accidentes de tránsito al día [3]. Lo que equivale a 5 muertes diarias en las carreteras del país [3]. A continuación, se describen las causas que alcanzaron el 64% de las causas que provocaron mayor número de accidentes de tránsito en el país: con un 64% fueron: impericia e imprudencia del conductor (33%), no respetar las señales de tránsito (21%); causas desconocidas (10%)[2].
El problema de los accidentes de tránsito se deben a tres factores; el factor humano, el factor mecánico y el factor ambiental [4]. El interés de este artículo es enfocarse en el factor ambiental que involucra el diseño geométrico de la vía. Una carretera correctamente diseñada, es aquella que le proporciona al usuario un alto grado de seguridad, tanto en el diseño geométrico, como en la señalización que se coloque a lo largo de la carretera para advertir de los posibles peligros y límites a los que debe de regirse el conductor[5]. El diseño de una vía atienden principalmente a los elementos de alineamientos rectos, curvas horizontales, sobreanchos, islas, canalización, carriles de cambio de velocidad[5], estos elementos, definen las características geométricas de la vía y están íntimamente ligados a la forma en que los vehículos pueden utilizarla; su comportamiento en la vía; la armonía entre la estética y funcionalidad de todos los elementos urbanos; y, a la presencia de los peatones con sus deseos de circulación[5]. Es difícil evaluar la incidencia de los elementos geométricos de la vía en los accidentes de tránsito. Por esto para poder encontrar la relación de algunos de estos elementos geométricos de la vía con los accidentes de tránsito se ha planteado el uso de técnicas de Inteligencia Computacional (IC). La inteligencia computacional, ha avanzado mucho en la actualidad y son muy efectivas en casos de toma de decisiones a partir de experiencias pasadas, ya que las técnicas de IC imitan el aprendizaje, de una persona. Una de las técnicas de IC son las Redes Neuronales Artificiales, las mismas permiten realizar una evaluación de modelos de predicción y se las puede aplicar a la estimación del número de accidentes posibles en una vía dependiendo de elementos geométricos de la misma.
Las Redes Neuronales Artificiales consisten en un algoritmo que emula el comportamiento del sistema nervioso animal. Este tipo de técnicas han demostrado tener buenos resultados tanto en la predicción como en la clasificación de series de datos [6]. Las Redes Neuronales constituyen una herramienta de análisis, modelación y predicción que se puede encontrar cómodamente integrada en muy diversos campos: robótica, ingeniería psicología y otros. Según sus múltiples aplicaciones en; reconocimiento de caracteres, conversión de texto a voz, reconocimiento de patrones en imágenes, problemas de combinatoria [7], las redes neuronales artificiales son vistas como herramientas de la ingeniería, que replican el pensamiento racional[8]. En todos los casos las redes se rigen por la filosofía general de obtener modelos coherentes con la realidad observada, de tal modo que sean los datos que determinen el comportamiento de la red [9].
Las Redes Neuronales Artificiales imitan el comportamiento del sistema neuronal del cuerpo humano, encontramos tres elementos principales: los órganos receptores que son los encargados de recoger la información del exterior; el sistema nervioso que transmite, analiza y en parte almacena la información elaborada, y los órganos efectores que reciben la información de parte del sistema nervioso y la convierte en una cierta acción (Dibike & Solomatine, n.d.) tomado de (Castellano Méndez, 2009). Aplicando esto en la RNA modelada se van a ingresar los datos de accidentes registrados en años anteriores como información del exterior, para entrenar la red neuronal con los datos de los elementos geométricos de la vía en el lugar que se generaron y así obtener datos de salida de accidentes futuros [8]. Los modelos de Redes Neuronales Artificiales tienen como una de sus principales características tratar incertidumbres de fácil adaptabilidad a nuevos datos y abstraen el conocimiento físico de los sistemas a ser modelados, ya que el modelo puede ser generado únicamente a partir de datos de entrada y salida [10]. El interés de las RNA no reside solamente en el modelo del elemento procesador sino en las formas en que se conectan estos elementos procesadores, generalmente los elementos procesadores están organizados en grupos llamados niveles o capas. Una red típica consiste en una secuencia de capas con conexiones entre capas adyacentes consecutivas [7].
En el campo de la vialidad las RNA se han aplicado para predecir velocidades[11][12], predicción de accidentes de tráfico[13], también para “Establecer la factibilidad de implementar el sistema de semáforos inteligentes” [14]. Se han utilizado para determinar la velocidad en vías con fiscalización electrónica de la velocidad, para reproducir la velocidad de los vehículos antes, después y en el mismo dispositivo fiscalizador, buscando observar el comportamiento del tráfico en trechos fiscalizados [15], para Modelar a partir de Redes Neuronales Artificiales la deforestación asociada a nuevos proyectos de infraestructura vial en las regiones del Nordeste y Bajo Cauca del departamento de Antioquia [16]. Sin embargo, como podemos ver no existen aplicaciones con respecto a buscar la relación entre el diseño geométrico de la vía y los accidentes de tránsito, probablemente por limitaciones en la información disponible.
La aplicación de las RNA, nos permitirán analizar ciertos elementos geométricos de las vías rurales y su incidencia en los accidentes de tránsito. Por lo que el objetivo de esta investigación es aplicar RNA en el modelamiento de la predicción del número de siniestros, lo cual incide en la seguridad vial, esta investigación busca emplear las RNA con el fin de obtener mejores resultados y obtener predicciones, no solo clasificaciones, para poder contribuir con un conjunto de modelos que sean un real aporte al estudio de la seguridad vial. En este trabajo se presentará un análisis preliminar de los datos, es decir, su pre- procesamiento, para el diseño de los modelos de estimación. En esta etapa se determinan el registro del número de accidentes por año, un análisis de las vías y la obtención de elementos geométricos como son los radios y pendientes utilizando datos de 7 años de estudio, desde 2014 hasta el 2020, información obtenida de la Agencia Nacional de Transito.
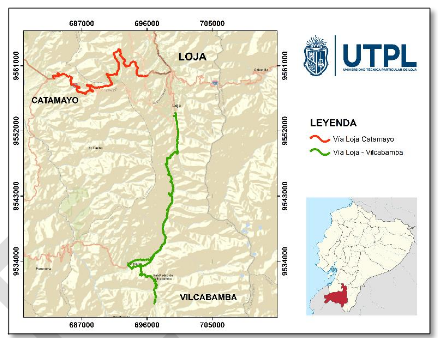
La metodología consistirá, en recolectar datos de accidentes en dos ejes viales distintos, la vía Loja – Catamayo y la vía Loja – Vilcabamba, en los lugares que se suscitan los accidentes se analizará el diseño de la vía, determinando los datos de radios de curvatura y pendientes con estas variables se formaran matrices que luego serán analizadas en el programa Matlab. El programa Matlab cuenta con una herramienta de RNA muy flexibles que permite realizar cambios en los entrenamientos, una vez encontrada la mejor arquitectura de la RNA, se modelará un sistema de predicción con un tramo de la vía y se revisara la validez del modelo por medio de métodos estadísticos de error.
2. Metodología
2.1. Área de estudio
Las vías utilizadas para esta investigación se encuentran ubicadas al sur del Ecuador en la provincia de Loja. La vía Loja- Catamayo pertenece a la red vial (E 50) y la vía Loja-Vilcabamba perteneciente al eje vial E682. En la tabla 1 se indican las coordenadas UTM de los ejes viales utilizados, y en la figura 1 se muestra la zona de estudio
Tabla 1. Coordenadas ejes viales
| Vía | Coordenadas UTM | |||
| Inicio | Fin | |||
| Loja-Vilcabamba | 4°01'57.70'' S | 79°11'56.83'' W | 4°15'2.12'' S | 79°13'30.28'' W |
| Loja- Catamayo | 3°58'45.42'' S | 79°12'46.37'' W | 4°0'23.56'' S | 79°22'25.21'' W |
Figura 1. Vías de la zona de estudio
2.2 Definición de variables
Se usaron datos de accidentes de tránsito ocurridos en las vías Loja-Vilcabamba y Loja- Catamayo entre los años 2014, 2015, 2016, 2017, 2018, 2019, y los meses de enero, febrero, marzo abril y mayo del año 2020, se emplearon los datos de radios de curvatura y las pendientes, obtenidos del Ministerio de Transporte y Obras Públicas
2.3 Materiales
Para la realización del diseño del proyecto se tomó en cuenta el Software de programación MATLAB, versión 2013. Debido a que presenta su interface sencilla y entendible para el usuario. Además, este software cuenta con procedimientos que involucran a redes neuronales artificiales como el Toolbox de Matlab Neural Network. Adicionalmente el Software ArcGIS y software Civil 3D. Adicionalmente se tomó en cuenta la base de datos de accidentes de tránsito proporcionados por la Unidad de Control Operativo de Tránsito (UCOT), del mismo modo se utilizaron las fuentes de información de las vías Loja- Vilcabamba, y Loja- Catamayo, entregadas por el Ministerio de Transporte y Obras Públicas Loja.
Identificación de variables de entrada
Las variables de entrada para la red serán los elementos geométricos de la vía radios y pendientes.
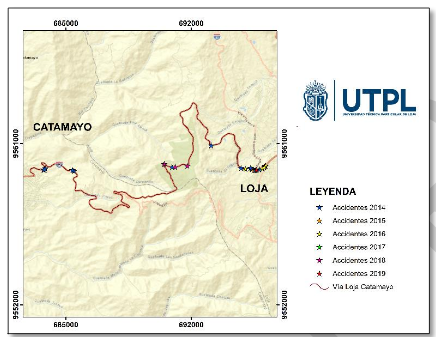
En la Figura 2 se observa la implantación de los accidentes en la vía Loja-Vilcabamba.
Figura 2. Accidentes vía Loja-Vilcabamba
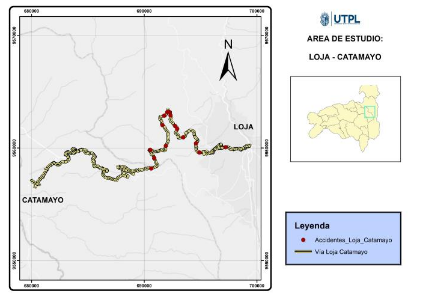
En la Figura 3 se observa la implantación de los accidentes en la vía Loja-Catamayo
Figura 3. Accidentes vía Loja- Catamayo
2.4 Implementación de arquitecturas de redes neuronales
La herramienta del programa Matlab a utilizarse permite cambiar el número de capas, número de neuronas, su función de activación tiene diversos tipos de interconexión entre capas, diversas funciones de error para optimizar la red, varios tipos de algoritmos de aprendizaje. Todas estas opciones son programables.
Una opción que se ha utilizado del toolbox es la diferenciación interna entre muestra de entrenamiento, validación y predicción o test. La red se entrena con los datos de entrada y va calculando una varianza dentro de los cuadrados medios del error, habitualmente representada por MSE (Mean Square Error) o MSW (Mean Square Within) que se calcula como la media de las k varianzas muestrales. MSE es un cociente: al numerador se le llama suma de cuadrados del error y se representa por SSE y al denominador grados de libertad por ser los términos independientes de la suma de cuadrados [17]. Debido al aprendizaje en cada iteración, este MSE de entrenamiento va disminuyendo. Paralelamente el programa va calculando el MSE con los datos de validación que globalmente van disminuyendo hasta cierto punto y luego aumentan paulatinamente. En ese punto Matlab automáticamente detiene el entrenamiento de la red, debido a que la red se está sobreentrenando para los datos de entrenamiento, pero se está distanciando de datos que no hayan intervenido en su entrenamiento. Esta característica se llama “early stopping” y evita la especialización de la red, lo cual es poco deseable para la generalización deseada. [17]
2.5 red aplicada
Se aplicó la red Perceptrón Multicapa, es una red de varias capas. Las capas son las de entrada, una o varias intermedias u ocultas y la de salida. Mediante el toolbox de Matlab se puede optar por varias capas ocultas, pero esto podría llevar a una red muy específica o sobreentrenada. Se trabajó con un entrenamiento supervisado estos algoritmos requieren el emparejamiento de cada vector de entrada con su correspondiente vector de salida. El entrenamiento consiste en presentar un vector de entrada a la red, calcular la salida de la red, compararla con la salida deseada, y el error o diferencia resultante se utiliza para realimentar la red y cambiar los pesos de acuerdo con un algoritmo que tiende a minimizar el error.
La red multicapa feedfoward se utilizó para el modelamiento porque esta permitió una prealimentación de las conexiones, todas las neuronas de la capa inmediatamente posterior [18], las señales neuronales se propagan hacia adelante a través de las capas de la red, comprende tres capas: entrada, intermedias u ocultas y de salida.
En la práctica no existe una regla definida para establecer el número inicial de neuronas y capas intermedias u ocultas, por lo que se realizó la metodología prueba-error. En nuestro caso se utilizaron dos arquitecturas de redes; en la primera arquitectura se trabajó con una neurona de entrada, 50 neuronas ocultas y una neurona de salida, en la segunda arquitectura se utilizó dos neuronas de entrada, 50 neuronas ocultas y una neurona de salida. En las Figuras 4 y 5 se observan las arquitecturas utilizadas.
Figura 4. Primer diseño de arquitectura aplicado
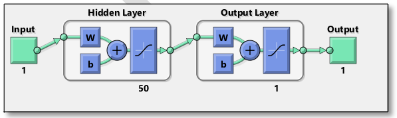
Figura 5. Segundo diseño de arquitectura aplicado
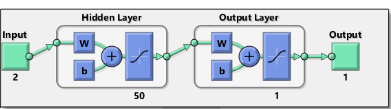
2.6 Preprocesamiento
El preprocesamiento de la base de datos se refiere al análisis y transformación de las variables de entrada y salida de la red para minimizar el ruido, enfatizando relaciones importantes, detectando tendencias, y aplanando la distribución de la variable para ayudar a la red neuronal en el aprendizaje de patrones relevantes[19] para esto se hizo el siguiente:
a) Se crearon archivos vectoriales georreferenciados de los accidentes de tránsito y se eliminaron los datos que estaban fuera de las vías de estudio.
b) Se generó un abscisado para cada vía, ubicando los accidentes para determinar los elementos geométricos existentes en cada vía.
2.7 Modelamiento determinístico de los accidentes de tránsito
a) Determinar las variables de los modelos a emplear, Loja-Vilcabamba (vía 1) y Loja-Catamayo (vía 2).
b) Simular el modelo elegido.
c) Analizar la bondad de los modelos.
Se realizaron cuatro alternativas de red neuronal artificial; la primera entrenando la red con los datos de los elementos geométricos (radios y pendientes) de la de la vía 1, comparando con la simulación de la vía 2. En la segunda alternativa se trabajó con el total de datos uniendo la vía 1 y la vía 2, se utilizó el 60%, 75%, 80% y 90% de los datos para entrenamiento de la red dejando el porcentaje restante para la comprobación con los datos simulados. En la tercera alternativa se agruparon los datos de los radios y así se analizó por rangos, en el caso de las pendientes no se lo realizo ya que no tiene un mayor rango. En la cuarta alternativa se utilizó dos capas de entrada de la red los radios y pendientes, para obtener una capa de salida. Los datos se agruparon de tal forma que siguieran una serie cronología anual establecida.
Durante la etapa de entrenamiento de las redes, se determina iterativamente los pesos de las conexiones, wji que conectan a las neuronas de entrada con las de la capa oculta y wj para la transferencia entre la capa oculta y la de salida. A partir de los datos de entrada la red en cada iteración genera una salida, a través de las neuronas que la componen, con los pesos y función de transferencia considerada, esta salida es comparada con los valores objetivos (accidentes observados), obteniéndose así un error. Esta fase concluye cuando la red converge y es capaz de minimizar el error. La función de transferencia y activación ha sido la del tipo sigmoidea.
El tolbox de Matlab cuenta con diversos algoritmos de entrenamiento de las redes entre los cuales esta TRAINBR (Bayesian regulation backpropagation), TRAINLM (Levenberg-Marquardt backpropagation), TRAINRP (Resilient backpropagation), trainscg (Scaled conjugate gradient backpropagation), y algunos más cuya función es entrenar la red, en el diseño se utilizó el TRAINBR [17].
Se aplicó un método de entrenamiento supervisado. A la red se le presenta parejas de patrones, un patrón de entrada emparejado con un patrón de salida deseada. Por cada presentación los pesos son ajustados de forma que disminuya el error entre la salida deseada y la respuesta de la red. El algoritmo de aprendizaje backpropagation conlleva una fase de propagación hacia adelante y otra fase de propagación hacia atrás. Ambas fases se realizan por cada patrón presentado en la sesión de entrenamiento[7].
La unidad procesadora j obtiene la cantidad Sj según la ecuación ( 1)
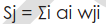
y genera la salida o nivel de activación según la ecuación (2)
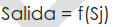
La función f es una función umbral genérica, entre las que cabe destacar la función Sigmoidal y la función Hiperbólica.
El valor de la salida de la unidad j es enviado o transmitido a lo largo de todas las conexiones de salida de dicha unidad.
Se usó el algoritmo de entrenamiento TRAINBR (Bayesian regulation backpropagation) que presenta un proceso de optimización, una vez obtenidos los datos de accidentes futuros se realizó la evaluación de los resultados.
2.8 Criterios de evaluación
Para el criterio de evaluación para medir la eficiencia de la red, se ha considerado utilizar el Error Cuadrático Medio (ECM). En este caso se define como la diferencia entre la salida de la red y la respuesta deseada. El cual se usa como factor de culminación del entrenamiento
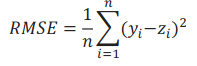
Donde “n” representa el número de elementos que intervienen en el pronóstico, “yi” representa el valor real y “zj” representa la salida pronosticada.
También se utilizó la función de eficiencia de Nash- Sutcliffe.
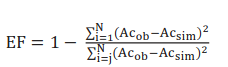
Donde EF: representa la eficiencia de Nash- Sutcliffe. 〖Ac〗_sim: Accidentes simulados, Ac_ob : Accidentes observados, Ac_ob: Promedio de los accidentes observados.
Para lo cual se establecieron los modelos con una cantidad de (50) neuronas ocultas en la capa oculta o intermedia. Las iteraciones en los modelos varían desde 600 a 1000 dependiendo del modelo y el proceso que le tome en converger al mejor resultado.
3. Resultados
3.1 Alternativa 1
En la primera alternativa se aplicó una capa de entrada, 50 neuronas ocultas y una capa de salida. 1
Opción (i).
Capa de entrada: se utilizó los datos de los radios de curvatura de la vía Loja-Vilcabamba.
Target: se utilizaron los datos de accidentes de la vía Loja- Vilcabamba,
Simulación: datos de los radios de curvatura de la vía Loja-Catamayo.
Capa de salida: se obtienen los datos de accidentes de la vía Loja- Catamayo.
Tabla 2. Errores de la alternativa I- opción (i)
| Alternativas | Coeficiente de eficiencia de Nash & Sutcliffe | Error cuadrático medio | ||
| Opción 1 | EF= | -0.167 | ECM= | 1.175 |
Figura 6. Accidentes futuros alternativa I- opción (i).
Opción (ii).
Capa de entrada: se utilizó los datos de las pendientes de la vía Loja-Vilcabamba.
Target: se utilizaron los datos de accidentes de la vía Loja-Vilcabamba.
Simulación: datos de las pendientes de la vía Loja-Catamayo.
Capa de salida: se obtienen los datos de accidentes de la vía Loja- Catamayo.
Tabla 3. Errores de la alternativa I- opción ii
| Alternativas | Coeficiente de eficiencia de Nash & Sutcliffe | Error cuadrático medio(RMSE) |
| Opción 1 | -2.604 | 2.119 |
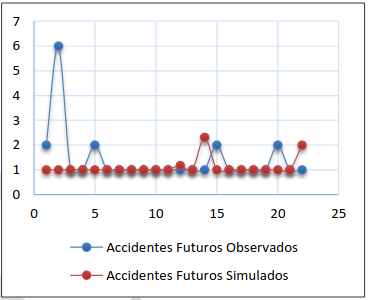
Figura 7. Accidentes futuros alternativa I- opción (ii).
3.2 Alternativa 2
En la segunda alternativa se unieron los datos de los radios y accidentes de las dos vías Loja-Vilcabamba y Loja-Catamayo, para trabajar con un mayor número de datos, utilizando para el entrenamiento de la red el 60%. 75%, 80% y 90%, como intento i, ii, iii, y iv respectivamente y el porcentaje restante se lo utilizó para comprobar la red.
Opción (i)
Capa de entrada: se utilizó los datos de los radios de curvatura de las dos vías, según el porcentaje de datos para entrenamiento.
Target: se utilizó los datos de accidentes de las dos vías, según el porcentaje de datos para entrenamiento.
Simulación: datos de los radios del porcentaje restante.
Capa de salida: se obtuvieron los datos de accidentes del porcentaje restante para la comprobación.
Tabla 4. Errores de la alternativa II-opción (i)
| Alternativas | Coeficiente de eficiencia de Nash & Sutcliffe | Error cuadrático medio (RMSE) |
| Intento 2 (60%) | -5.179 | 1.434 |
| Intento 1 (75%) | -4.463 | 0.209 |
| Intento 3 (80%) | -2.178 | 1.164 |
| Intento 4 (90%) | -1.610 | 1.909 |
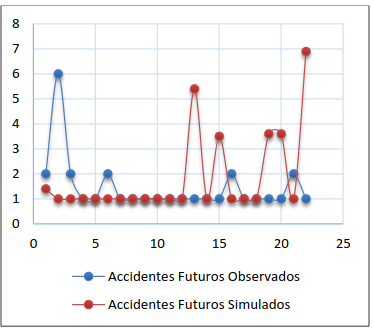
Figura 8. Accidentes futuros alternativa II- opción (i)-intento 1
Figura 9. Accidentes futuros alternativa II- opción (i)- intento 2
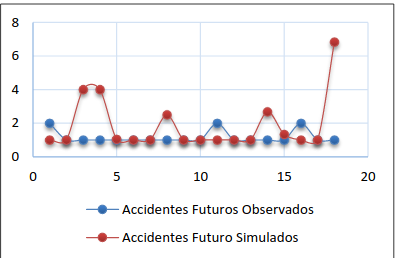
Figura 10. Accidentes futuros alternativa II- opción (i)- intento 3
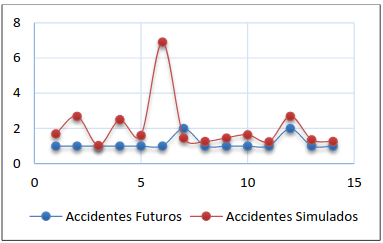
Figura 11. Accidentes futuros alternativa II- opción (i)- intento 4
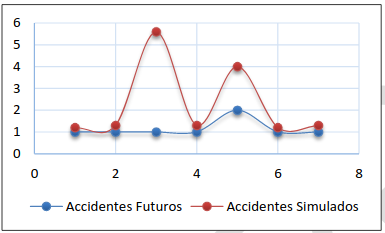
Opción (ii).
Capa de entrada: se utilizó los datos de las pendientes de las dos vías, según el porcentaje de datos para entrenamiento.
Target: se utilizó los datos de accidentes de las dos vías, según el porcentaje de datos para entrenamiento.
Simulación: datos de las pendientes del porcentaje restante.
Capa de salida: se obtuvieron los datos de accidentes del porcentaje restante para la comprobación.
Tabla 5. Errores de la alternativa II-opción (ii)
| Intento # Alternativas | Coeficiente de eficiencia de Nash & Sutcliffe | Error cuadrático medio (RMSE) | |
| 1 (60%) | EF= | -1.189 | 2.138 |
| 2 (75%) | EF= | -1.310 | 0.614 |
| 3 (80%) | EF= | -0.975 | 0.755 |
| 4 (90%) | EF= | -2.046 | 2.712 |
Figura 12. Accidentes futuros alternativa II- opción (ii)- intento 1
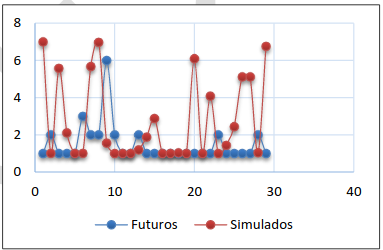
Figura 13. Accidentes futuros alternativa II- opción (ii)- intento 2
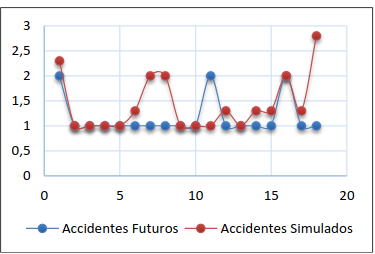
Figura 14. Accidentes futuros alternativa II- opción (ii)- intento 3
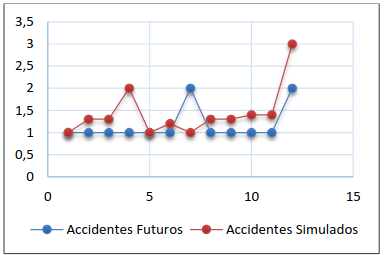
Figura 15. Accidentes futuros alternativa II- opción (ii)- intento 4
3.3 Alternativa 3
En la tercera alternativa se agruparon los valores de los radios sumando los accidentes pertenecientes a cada rango, entrenando la red con datos de la vía Loja-Vilcabamba, y simulando para la vía Loja-Catamayo obteniendo los accidentes.
Opción (i)
Capa de entrada: se utilizó los datos de los radios de curvatura de la vía Loja-Vilcabamba agrupado de 20 en 20.
Target: se utilizaron los datos de accidentes de la vía Loja- Vilcabamba.
Simulación: datos de los radios de curvatura agrupado de la vía Loja-Catamayo.
Capa de salida: se obtienen los datos de accidentes de la vía Loja- Catamayo.
Tabla 6. Errores de la alternativa III-opción (i)
| Alternativa | Coeficiente de eficiencia de Nash & Sutcliffe | Error cuadrático medio (RMSE) |
| Intento 1 | -0.722 | 4.352 |
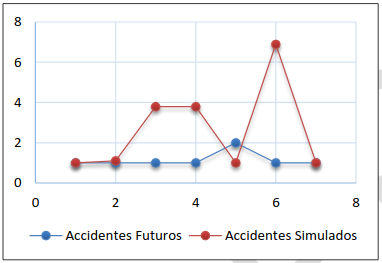
Figura 16. Accidentes futuros alternativa III- opción (i)
Opción (ii)
Capa de entrada: se utilizó los datos de los radios de curvatura de la vía Loja-Vilcabamba agrupado de 40 en 40.
Target: se utilizaron los datos de accidentes de la vía Loja- Vilcabamba.
Simulación: datos de los radios de curvatura agrupado de la vía Loja-Catamayo.
Capa de salida: se obtienen los datos de accidentes de la vía Loja- Catamayo
Tabla 7. Errores de la alternativa III-opción (ii)
| Alternativa | Coeficiente de eficiencia de Nash & Sutcliffe | Error cuadrático medio (RMSE) |
| Intento 2 | -3.245 | 1.924 |
Figura 17. Accidentes futuros alternativa III- opción (ii)
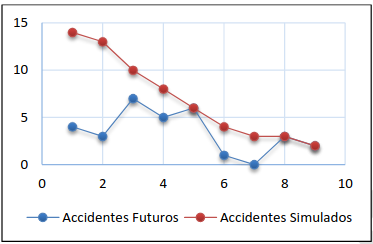
3.4 Alternativa 4
En la cuarta alternativa se aplicó una arquitectura con dos capas de entrada, los datos de radios de curvatura y pendientes, 50 neuronas ocultas y una capa de salida.
Opción (i).
Capa de entrada: Se manejó los datos de los radios de curvatura y pendientes de la vía Loja-Vilcabamba.
Target: Se aplicaron los datos de accidentes de la vía Loja- Vilcabamba,
Simulación: Datos de los radios de curvatura y pendientes de la vía Loja-Catamayo.
Capa de salida: Se obtienen los datos de accidentes de la vía Loja- Catamayo.
Tabla 8. Errores de la alternativa IV-opción (i)
| Alternativa | Coeficiente de eficiencia de Nash & Sutcliffe | Error cuadrático medio (RMSE) |
| Intento 2 | -0.513 | 5.121 |
Figura 18. Accidentes futuros alternativa IV- opción (i)
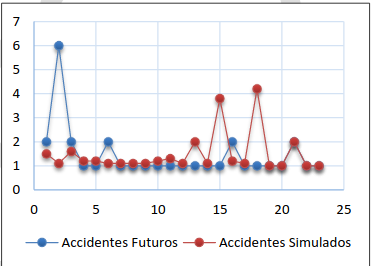
Opción (ii).
Capa de entrada: Se utilizó los datos de los radios de curvatura y pendientes unido de las dos vías Loja-Vilcabamba y Loja-Catamayo, para trabajar con un mayor número de datos, utilizando para el entrenamiento de la red el 75%, de datos y el porcentaje restante se lo utilizó para comprobar la red.
Target: Se utilizaron el 75% de datos de accidentes de las dos vías.
Simulación: El 25% de datos de los radios de curvatura y pendientes de las dos vías en estudio.
Capa de salida: Se obtienen los datos de accidentes restantes.
Tabla 9. Errores de la alternativa IV-opción (ii)
| Alternativa | Coeficiente de eficiencia de Nash & Sutcliffe | Error cuadrático medio (RMSE) |
| Intento 1 | -0.77 | 1.40 |
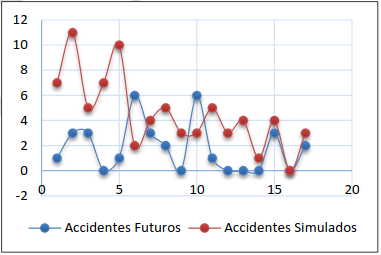
Figura 19. Accidentes futuros alternativa IV- opción (ii)
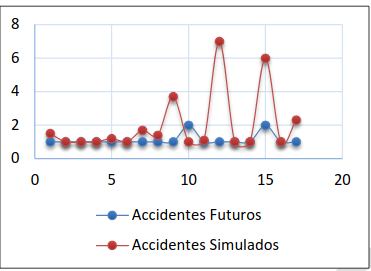
4. Análisis de resultados
En los criterios de evaluación la eficiencia de Nash- Sutcliffe, los valores más cercanos a 1 indican un ajuste perfecto entre la simulación y los valores observados, y en el error cuadrático medio los valores entre más cercanos a cero indican que el error es bajo, examinando los resultados obtenidos a pesar de las varias iteraciones no se cumplieron estos criterios por lo que se puede concluir que la RNA no fue aplicable, esto se puede dar por las siguientes razones:
Constancia paramétrica: El proceso en análisis pocas veces es estable, lo que lleva a grandes errores. Cuando esto ocurre, los modelos que antes eran exitosos fallan en pronósticos cuando surgen datos atípicos. La constancia paramétrica es esencial para el diseño del modelo. Requiriéndose que los parámetros sean estadísticamente estables [20].
Subentrenamieto de la Red por falta de datos. En la mayoría de los casos a pesar de la que la geometría de la vía es crítica se registra un solo accidente, por lo que imposibilita la necesidad de cambio en los pesos de las conexiones y el entrenamiento de la RNA es mínimo.
La razón principal es que los accidentes aparentemente no se deben a la geometría de la vía, si no a elementos como exceso de velocidad, impericia del conductor, que no se registran en los datos del accidente y que no pueden expresarse como variables y por ende no pueden entrar en el modelo.
Conclusiones
En base a investigaciones recientes sobre accidentes de tránsito analizados a través de las RNA se estableció el marco teórico de la investigación.
A partir de la información proporcionada por la UCOT se obtuvo 110 datos de accidentes de tránsito q ocurridos en los últimos 7 años en las vías Loja-Vilcabamba y Loja-Catamayo.
Se determinaron los elementos geométricos de la vía en los puntos donde ocurrieron los accidentes, los mismos fueron 71 radios y pendientes.
Se aplicaron las redes neuronales artificiales para el análisis de variables relacionadas a los elementos geométricos de una carretera de montaña que afectan en la seguridad vial e inducen a los accidentes de tránsito.
Se diseñó en Matlab dos arquitecturas de redes: la primera con una capa de entrada, 50 ocultas y una capa de salida, la otra arquitectura con dos neuronas de entrada, 50 ocultas y una capa de salida.
Con la comprobación de la validez de los modelos aplicados, se determinó que no fue posible aprobar los pronósticos ya que los resultados de los criterios de evaluación fueron bajos en varias alternativas calculadas.
Se recomienda que se realice la predicción con más capas de entrada tomando en cuenta elementos como radios de curvatura, pendientes, longitudes tangenciales, velocidades de operación, con estas entradas se podría tener una mejor respuesta.
Referencias
- World Health Organization, “Global Status Report on Road Safety 2015,” 2015.
- Instituto Nacional de Estadísticas y Censos, “Anuario de Estadísticas de Transportes 2014,” 2014. doi: 10.1017/CBO9781107415324.004.
- J. A. Castillo Guerra, Diana Mabell; Herrera Bolaños, Rafael Alfredo; Muñoz Abril, “Tesis para optar por Título de Ingeniero en Gestión Empresarial ‘Análisis de los Factores que Inciden en los Accidentes de Tánsito Del Servicio de Transportación Pública Interprovincial en el Ecuador,’” UNIVERSIDAD DE GUAYAQUIL FACULTAD, 2013.
- J. Gonzalez and J. Ordoñez, “Estudio de los factores que intervienen en los accidentes e infracciones de tránsito ocasionados por los buses de transporte público de pasajeros tipo urbano en la ciudad de Cuenca y planteamiento de la propuesta para disminuirlos,” UNIVERSIDAD POLITÉCNICA SALESIANA, SEDE CUENCA, 2014.
- J. A. Villacorta Delgado, ““Los accidentes de tránsito y su relación con las caracteristicas geometricas de avenida Heroés del Cenepa desde la avenida Independencia hasta la avenida Vía de Evitamiento Sur en la ciudad de Cajamarca",” Universidad Nacional de Cajamarca, 2008.
- J. M. L. S. Montt, Cecilia; Rubio, “Análisis de accidentes de tránsito con inteligencia computacional,” Congr. Chil. Ing. Transp., no. 16, p. 11, 2013.
- X. Basogain Olabe, “Redes Neuronales Artificiales y sus Aplicaciones,” 2004.
- K. Carpio Pelaez, “Aplicación de redes neuronales para la modelización y generación de series hidrológicas,” Universidad Tecnica Particular de Loja, 2014.
- M. Castellano Méndez, “Modelización, estadística con Redes Neuronales. Aplicaciones a la Hidrología, Aerobiología y Modelización de Procesos,” 2009. https://docplayer.es/amp/29334570-Modelizacion-estadistica-con-redes-neuronales-aplicaciones-a-la-hidrologia-aerobiologia-y-modelizacion-de-procesos.html.
- R. Ballini, S. Soares, and M. G. Andrade, “Previsão de vazões médias mensais usando redes neurais nebulosas,” Control. Autom., vol. 14, no. 3, pp. 286–297, 2003, doi: 10.1590/s0103-17592003000300008.
- J. McFadden, W. T. Yang, and S. R. Durrans, Application of artificial neural networks to predict speeds on two-lane rural highways, no. 1751. National Research Council, 2001, pp. 9–17.
- M. R. Rojas Godoy, “Predicción de accidentes de tránsito utilizando redes neuronales artificiales y cuckoo search,” 2015. Accessed: Aug. 17, 2020. [Online]. Available: http://opac.pucv.cl/pucv_txt/txt-7500/UCE7824_01.pdf.
- K. S. Jadaan, M. Al-Fayyad, and H. F. Gammoh, “Prediction of Road Traffic Accidents in Jordan using Artificial Neural Network (ANN),” doi: 10.12720/jtle.2.2.92-94.
- C. O. Natarerno Yanes, “Inteligencia artificial aplicada al tránsito en la cuidad de guatemala utilizando redes neuronales,” p. 84, 2013.
- C. W. Rengifo Bocanegra, H. B. Bettela Cybis, M. A. Prudêncio Jacques, and M. Tassinari Stumpf, “Modelo de Redes Neuronales Artificiales para determinar la velocidad en vías con fiscalización electrónica de la velocidad.”
- L. F. Gómez Ossa, “Aplicación de Redes Neuronales Artificiales en la Modelación de la Deforestación Asociada a Nuevos Proyectos de Infraestructura Vial en las Regiones del Nordeste y Bajo Cauca del Departamento de Antioquia,” 2014.
- M. A. Jiménez, “Implementación en MATLAB de técnicas matemáticas en el análisis de experimentos,” ETSIA, 2008.
- A. Moreno, “Desarrollo de una interfaz gráfica de redes neuronales usando Matlab”,” UNIVERSIDAD CARLOS III MADRID, 2000.
- Y. A. Vidaurre Siadén, “Aplicación de las Redes Neuronales Artificiales para el Pronóstico de la Demanda de Agua Potable en la Empresa Epsel S.A de La Ciudad de Lambayeque,” 2012.
- S. Makrisdakis, Spyros;Hyndman, Rob J; Wheelwright, Forescasting Methods and Aplications, Third. 1998.