1. Introducción
Las matemáticas constituyen un elemento clave en el desarrollo de innovaciones en ingeniería, por lo cual su estudio es obligatorio ieros. Sin embargo, es el principal obstáculo para que los jóvenes se decidan a estudiar ingeniería, o en su defecto, deserten de la carrera, que en Colombia supera el 45 % 1.
Los motivos que producen esta problemática son varios, entre los cuales se destacan la falta de desarrollo de competencias matemáticas en los estudiantes (situación que se origina en la educación media), la falta de una educación matemática acorde con las realidades de los estudiantes, entre otros factores, que forman parte del estudio que motivó este trabajo de investigación 2.
Así las cosas, falta coherencia entre lo declarado en una asignatura del ciclo básico de ingeniería, como álgebra lineal, y lo establecido universalmente en los sílabo de estos programas en las Instituciones de Educación Superior (IES), ya que un alto porcentaje de los programas de ingeniería han reducido el contenido de esta asignatura a cuatro unidades básicas (vectores, matrices, determinantes y sistemas de ecuaciones), omitiendo temas que por sus características son esenciales en la comprensión y desarrollo de temáticas propias de semestres avanzados, como la investigación de operaciones, ecuaciones diferenciales, entre otras.
Según Hoffman 3, el álgebra lineal es una rama de las matemáticas que trata de las propiedades comunes de los sistemas algebraicos, que constan de un conjunto más una noción razonable de combinación lineal de los elementos del conjunto. Justamente esta última parte es la que han omitido la mayoría de los programas académicos, como se muestra en la Figura 1.
Figura 1
Número de IES que cuentan con contenido básico y completo de álgebra lineal. Fuente. Elaboración propia.
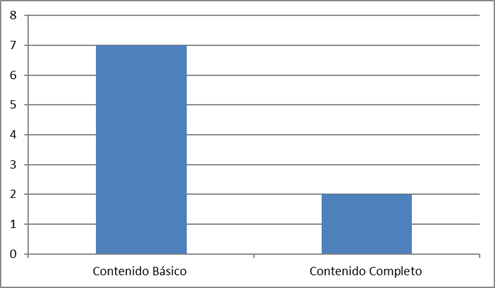
En la anterior figura se muestran los resultados del estudio realizado en las 11 facultades de ingeniería que ofertan programas en la ciudad de Barranquilla de manera presencial. En dos de ellas álgebra lineal no forma parte del plan de estudios o está integrada a otra asignatura. Para el análisis de los contenidos se diseñaron dos categorías: la primera, llamada contenido básico (vectores, matrices, sistemas de ecuaciones), y la segunda, contenido completo (básico más espacios vectoriales, transformaciones lineales, autovalores, auto vectores diagonalización, triangularización, formas de Jordan). Se evidencia que el 78 % de los contenidos de álgebra lineal están en la categoría “contenido básico”, correspondiente a siete de las nueve facultades en las que forma parte del plan de estudios, es decir, el 22 % se ubican en “contenido completo”, equivalente a dos facultades.
Lo anterior, es consecuencia de una práctica que busca simplificar los contenidos para hacer la carrera menos compleja para el estudiante y a partir de allí tratar de disminuir el trabajo independiente, ayudando de alguna manera a disminuir los indicadores de deserción o repitencia. Sin embargo, la simplificación de contenidos impacta de una forma negativa el desarrollo de competencias matemáticas abstractas en el estudiante de ingeniería, lo cual, según el informe “Ecuaciones y desigualdades: hacer las matemáticas accesibles a todos” de la Organización para la Cooperación y el Desarrollo Económico (OCDE), “la falta de acceso a contenidos matemáticos en clase puede dejar a los jóvenes en desventaja económica y social de por vida” 4, es decir, el hecho de construir contenidos programáticos básicos es en realidad una desventaja para los ingenieros en formación. El mismo informe plantea que los mejores resultados académicos y en pruebas internacionales los obtienen estudiantes con formación en matemáticas puras y abstractas, además de existir un diferencial de dos años de formación académica entre quienes estudian una matemática pura y quienes no.
Esto pone en evidencia dos necesidades: diseñar contenidos completos en los cuales se estudien las temáticas propias del álgebra lineal y elaborar estrategias que permitan el estudio de una matemática pura en los contenidos de las asignaturas del ciclo básico de ingeniería.
1.1 Relación del álgebra lineal con la ingeniería
En esta sección se analiza la importancia del álgebra lineal en relación con varias aplicaciones propias de distintas ramas de la ingeniería, lo cual justifica el hecho de haberla considerado para la elaboración de esta propuesta.
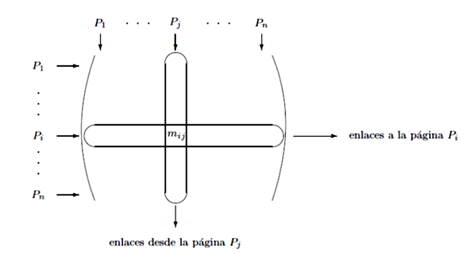
Para comenzar, se toma la teoría de grafos y redes. Una red es la unión de puntos, nodos, mediante líneas llamadas puentes, que visto como un todo se denomina grafo. La matriz asociada a un grafo es un arreglo de números definidos por la relación A ij =1 si hay un puente del nodo i al nodo j en el grafo. En caso contrario, el valor asignado es cero. Un ejemplo de este tipo de trabajo es lo que se plantea para el page rank, mecanismo por medio del cual el buscador Google asigna un orden específico al momento de mostrar los resultados de una búsqueda.
Inicialmente, se elabora una matriz con las características mencionadas, es decir, las páginas son vistas como nodos y si las dos están enlazadas se les coloca un valor de uno, en caso de no estarlo se asigna cero. Luego, mediante un proceso de búsqueda de autovalores y normalización, el resultado es un valor que proporciona las posiciones en la lista de resultados.
En estadística, al momento de analizar datos, a menudo el interés se enfoca en la matriz de correlación Aij = E [YiYj] de un vector aleatorio X = (X 1 , …, X n ) con Y i = X i - E [X i ] . Generalmente, esta matriz se deriva de datos y a veces, incluso, determina las variables aleatorias, si el tipo de la distribución es fijo 4.
Para el filtraje de datos. Dado un conjunto de puntos de datos, a menudo se desea ver tendencias o usar los datos para hacer predicciones. El álgebra lineal permite resolver este problema de manera elegante. Es posible aproximar puntos de datos usando cierto tipo de funciones. La misma idea funciona en dimensiones más altas, si se quisiera ver cómo depende un determinado punto de datos en dos conjuntos de datos. Un ejemplo de esto es el método de aproximación por mínimos cuadrados, por medio del cual es posible encontrar la función que asocia un conjunto de datos con una función matemática 5.
En las redes neuronales es posible mostrar un ejemplo de cómo el álgebra lineal tiene las redes Hopfield, que en el espacio de estado es un vector bidimensional. Cada estado de la red está dado por un vector x, en el que cada componente toma los valores -1 o 1. Si W es una matriz simétrica n × n, se puede definir un “mapa de aprendizaje” T : x → sign Wx, donde el signo se toma como componente. La energía del estado es el producto punto - (x, Wx) / 2. El interés de este tipo de estudios se basa en los puntos fijos 6.
Para los procesos de Markov. Supóngase que se tienen un dado y tres bolsas con 100 bolas cada una. Cuando se lanza el dado y aparece un 5, se mueve una bola de la bolsa 1 a la bolsa 2. Si el dado muestra 1 o 2, se mueve una bola de la bolsa 2 a la bolsa 3. Si es 3 o 4, se mueve una bola de la bolsa 3 a la bolsa 1 y otra de la bolsa 3 a la bolsa 2. Después de un tiempo, ¿cuántas bolas se espera tener en cada bolsa? Este es un ejemplo de un proceso de Markov, para el cual se construye una matriz de equilibrio. Aquí es importante conocer los autovectores asociados a la matriz mencionada 6.
Finalmente, en problemas inversos. Se usa para la reconstrucción de alguna función de distribución de probabilidad de la media. Esta herramienta se estudió por primera vez en 1917 y ahora es esencial para aplicaciones como diagnóstico médico, para la física o para aplicaciones astrofísicas. La reconstrucción también se denomina tomografía. Es una herramienta matemática desarrollada para la solución de este problema y conduce a la construcción de escáneres sofisticados. Es importante destacar que la inversión h = R (f) → f es rápida, precisa, robusta y requiere tan pocos puntos de datos como sea posible 5.
2. Metodología
En las clases de álgebra se aplicaron los conceptos de deconstrucción propios de la pedagogía de géneros literarios. En otras palabras, se consideró que una forma para lograr un mejor entendimiento de los temas que se integraron al contenido era mejorar la comprensión lectora de los estudiantes. Por esta razón, se tomó este componente para deconstruir los teoremas y corolarios que se comenzarían a estudiar.
Adicionalmente, se enseñó a los estudiantes a realizar demostraciones, de lo simple a lo complejo, hasta llegar a resultados más importantes. Por ejemplo, el teorema del núcleo y la imagen.
La estrategia se implementó en tres fases:
1. Trabajo integrado con el docente de competencias comunicativas
2. Tutorías semanales enfocadas en la forma de hacer demostraciones
3. Selección de aplicaciones junto con el docente de programación II
2.1. Fase 1
Con fundamento en la teoría de los géneros literarios de la escuela de 7, en la que se establecen varias etapas para la comprensión total de los textos (deconstrucción, construcción conjunta, construcción independiente) 8. En la etapa de deconstrucción se llevan a cabo las siguientes actividades:
- Estructura y propósito del texto
- Lectura detallada
- Re-representación de las ideas del texto
- Reacción al texto
De acuerdo con lo descrito, con la ayuda del profesor de competencias comunicativas se realizaron, de forma paralela a las clases, ejercicios de lecturas de textos matemáticos haciendo uso de las actividades correspondientes a la etapa de deconstrucción.
Por otra parte, en las clases de álgebra lineal se estudiaron las definiciones, proposiciones, teoremas y corolarios, de acuerdo con las actividades descritas. Un ejemplo es el referente a la siguiente proposición:
“Sea V un espacio vectorial sobre los reales con U y W subespacios de V, entonces:
a) U∩W es un espacio vectorial de V
b) El conjunto U+W={u+w : u ϵ U y w ϵ W} es un subespacio de V, denominado suma de U y W ”9
Para esta proposición se hizo la contextualización, recordando lo definición de un espacio vectorial y un subespacio vectorial, en especial los axiomas que determinan que un conjunto sea o no un espacio/subespacio vectorial, partiendo de la exploración de los saberes previos.
Así mismo, la estructura y propósito del texto se estudió a partir de las condiciones necesarias y suficientes, partiendo de la implicación lógica: si P entonces Q.
Seguidamente, se hizo la lectura detallada de la proposición con los elementos descritos. La re-representación exploró con un ejemplo práctico lo que sucedería si las condiciones de la proposición no se cumplen.
Finalmente, se analizaron las reacciones de los estudiantes al ver la proposición deconstruida y cómo podría enunciarse de una manera diferente.
2.2. Fase 2
Teniendo en cuenta aspectos como el resultado de Saber 11, IE de procedencia y el examen diagnóstico, se programaron horas de tutorías adicionales por grupos. El objetivo era explicar los elementos que se debían considerar para hacer una demostración. Este trabajo se adelantó con el apoyo de los docentes de ciencias básicas de la Facultad de Ingeniería.
2.3. Fase 3
Posteriormente, los estudiantes realizaron una búsqueda bibliográfica de las diversas aplicaciones en las cuales se hacía uso de conceptos del álgebra lineal, encontrado una gran variedad, especialmente en el área de sistemas y programación, con énfasis en la criptografía. Con ayuda del docente de la asignatura, los estudiantes construyeron una forma alternativa de la criptografía con matrices.
3. Resultados y discusión
En este aparte se evalúa la estrategia implementada, a partir del resultado al cual llegaron los estudiantes en la aplicación de álgebra lineal a la criptografía con matrices.
El uso de matrices para encriptar información se fundamenta en un procedimiento matemático derivado de las propiedades de los espacios de matrices cuadradas. Toda matriz cuadrada, con determinante diferente de cero, tiene inversa. El producto de la matriz con su inversa da como resultado la matriz identidad. Esta propiedad se usa para codificar información y son ejemplos didácticos para introducir al estudiante de sistemas en el campo del conocimiento que se articula con la seguridad informática, que es una de las líneas de investigación del programa de ingeniería de sistemas de la Corporación Universitaria Americana.
Las etapas son las siguientes:
El primer paso consiste en asignar a cada letra del alfabeto un número del 1 al 26, iniciando con A=1.
Posteriormente, los caracteres de la frase se remplazan por los números asignados. De esta manera el mensaje se convierte en una secuencia de números.
Luego, se construye una matriz con la secuencia de los números anteriores, de tal forma que se pueda multiplicar por otra matriz que se llamará “matriz candado”, es decir, el número de columnas de la matriz formada por la secuencia de números debe tener el mismo número de filas de la matriz candado.
Finalmente, se multiplican las matrices. El resultado se coloca en un vector y es el mensaje que se debe enviar.
Para decodificar la información basta con multiplicar el vector encriptado por la inversa de la matriz “candado”. Luego, se remplazan los números por las letras del alfabeto latino 10.
Sin embargo, posteriormente al estudio de base y dimensión de un espacio vectorial, en el que uno de los subtemas es el de vector de coordenadas, los estudiantes comenzaron a idealizar la forma de emplear este concepto matemático en la criptografía. A continuación, se muestra esta representación:
Paso 1.
Determinar la base del espacio vectorial K, que puede ser de la siguiente forma:
β={(a1,…,an ),(b1,…,bn )…(k)}
Conjunto de vectores linealmente independientes, que a su vez generan todo el espacio vectorial de dimensión k. A manera de ejemplo se tomó la base β={(1,0,1),(1,1,-1),(1,-1,0)}
Paso 2.
Asignar a cada palabra de la frase que se va a encriptar un número y de este conjunto de palabras codificadas se forma un vector.
Por ejemplo, ese escoge la palabra “cancelar el envío”
Cancelar=1
El=2
Envío=3
Con estos valores se forma el vector v=(1,2,3). Dicho vector se puede expresar como una combinación lineal de la base β={(1,0,1),(1,1,-1),(1,-1,0)} de la siguiente manera:
(1,2,3)= ∝1 (1,0,1)+∝1 (1,1,-1)+∝1 (1,-1,0)
Se realizan las operaciones de producto de un escalar por un vector, luego la suma de vectores y finalmente se igualan los componentes de los vectores, encontrando los valores para ∝1, ∝2, ∝3
∝1 = 3
∝2 = 0
∝3 = -2
Posteriormente, el vector v, expresado en función de la base β [v]β = (3,0,-2). Este último vector es encriptación de la información.
Para volver al vector original se realiza el siguiente procedimiento:
v=3(1,0,1)+(0)(1,1,-1)+(-2)(1,-1,0)=(1,2,3)
Que corresponde a la información dada inicialmente y al código asignado a cada palabra de la frase: 1 para “cancelar”, 2 para “el” y 3 para “envío”.
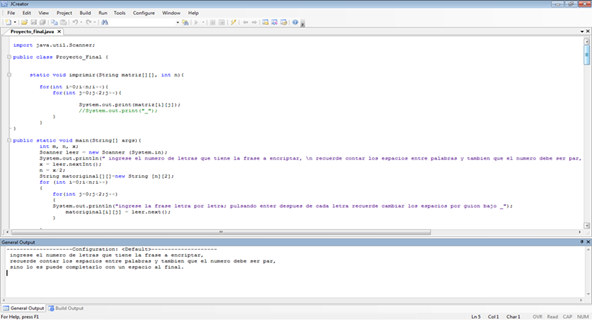
Luego de diseñar el mencionado método, un grupo de estudiantes realizó una pequeña aplicación en el programa JAVA, como se puede apreciar en las Figuras 3 y 4.
Figura 4
Imagen del código fuente de la aplicación para hacer criptografía. Fuente: elaboración propia.
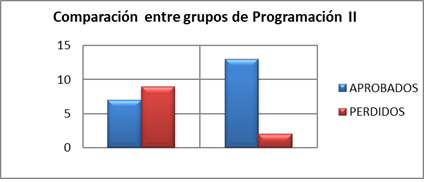
Las Figuras 2 y 3 son una muestra de la evaluación de la estrategia, evidencian cómo el uso de la misma coadyuvó en el mejoramiento del rendimiento académico de los estudiantes en otras asignaturas. En este caso, se presentó una mejora en los resultados en Programación II, en el que el número de estudiantes que no aprobó disminuyó considerablemente con respecto al semestre anterior.
La Figura 5 muestra cómo mejoró el rendimiento de los estudiantes en dos semestres. En el primero se nota que 9 de los 16 estudiantes no aprobaron la asignatura programación II. En el segundo, 13 de 15 superaron dicha asignatura.
4. Conclusiones
Este trabajo de investigación muestra los resultados de la implementación de una estrategia que integró varias asignaturas (álgebra lineal, competencias comunicativas y programación II). Fue una apuesta en la búsqueda por mejorar la calidad, a partir de una necesidad, y en ella convergieron varias necesidades que se vienen haciendo evidentes en las clases y que se pueden confirmar en el rendimiento académico.
Como principales conclusiones se tienen las siguientes:
Los resultados ratifican la importancia de la comprensión lectora en el desarrollo de competencias matemáticas en los estudiantes, como lo ratifican los trabajos realizados por Romero (2012) y Sandoval (2010).
El trabajo integrador entre varias asignaturas se muestra como una alternativa que motiva al estudiante a dar mejores resultados, como lo plantean Chávez, Martínez, & Cano (2014).
El mejoramiento de la calidad en las IES pasa por una revisión de las prácticas que se emplean en el aula y que, a su vez, implican la revisión de los contenidos y la forma como se vienen desarrollando.
Los contenidos de álgebra lineal en el 80 % de las IES que cuentan con facultades de ingeniería en Barranquilla no están acorde con lo consensuado universalmente sobre lo que debe incluir un curso de esta asignatura, como lo evidencia la estadística mostrada en la primera sección de este trabajo.
La estrategia demostró su viabilidad y con ella se alcanzaron los objetivos previstos para el curso.
Cabe destacar que la implementación de estrategias innovadoras en las aulas requiere un esfuerzo adicional, debido al bajo nivel de competencias matemáticas con las que ingresa un alto porcentaje de estudiantes a las IES. Sin embargo, luego de varias sesiones de tutorías fue posible evidenciar evoluciones positivas y un incremento en el nivel de competencias matemáticas.